Altın orana ilişkin matematik bilgisi ilk kez İ.Ö. 3. Yüzyılda Öklid’in Stoikheia ("Öğeler") adlı yapıtında "aşıt ve ortalama oran" adıyla kayda geçirilmiştir. Eldeki veriler,bu bilginin geçmişinin aslında Eski Mısır’da İ.Ö. 3000 yılına kadar dayandığını göstermektedir. Grek dünyasına da Pythagoras ve Pythagoras’cular tarafından tanıtıldığı ileri sürülür.Altın oran, (Fi) sayısı olarak bilinir. Bu sayı, Eski Yunan düşünürleri tarafından bulunmuştur, ancak Fi sayısını kimin tanımladığı kesin olarak belli değildir. Eski Yunan düşünürlerinin bazılarının, Fi sayısının yerine (to) sayısını kullandıkları da bilinmektedir.
İ.Ö. 500’lü yıllarda yaşamış olan tüm zamanların en büyük matematikçilerinden biri olan Pisagor , altın oranla ilgili aşağıdaki düşüncelerini dile getirmiştir:
Bir insanın tüm vücudu ile göbeğine kadar olan yüksekliğinin oranı, bir pentagramın uzun ve kısa kenarlarının oranı, bir dikdörtgenin uzun ve kısa kenarlarının oranı, hepsi aynıdır. Bunun sebebi nedir? Çünkü tüm parçanın büyük parçaya oranı, büyük parçanın küçük parçaya oranına eşittir.
Altın oran, günlük yaşantımızda, matematiğin estetik güzelliğe etki ettiği her alanda karşımıza çıkan bir kavramdır. Altın oranın çok çeşitli tanımları verilebilir ama altın oran, neticede matematiksel bir kavramdır ve değeri de 1,618033.... olarak devam eden ondalık bir sayıdır. Altın oranın matematiksel anlamına geçmeden önce altın oranın karşımıza çıktığı bazı alanlara değinelim.
Altın oran, örneğin bir dikdörtgenin göze en estetik gözükmesi için uzun kenarı ile kısa kenarı arasındaki orandır. Buna benzer olarak, bir doğru parçasının ikiye ayrıldığında göze en hoş gelen ikiye ayrılma oranıdır. Altın oran, sadece dikdörtgen ve doğru için değil, neredeyse tüm geometrik cisimler ve yapılar için kullanılabilir.
Altın oranın matematiksel açıdan basit bir tanımı şu şekilde yapılabilir:
Altın oran, 1 sayısına eklendiğinde kendi karesine eşit olan iki sayıdan biridir. Altın oran 1,618033.... olarak devam eden ondalık sayıdır. 1 sayısına eklendiğinde kendi karesine eşit olan diğer sayı da - 0,618033... olarak devam eden ondalık sayıdır.
Altın Oranın Görüldüğü Ve Kullanıldığı Yerler:
1) Ayçiçeği: Ayçiçeği'nin merkezinden dışarıya doğru sağdan sola ve soldan sağa doğru tane sayılarının birbirine oranı altın oranı verir.
2) Papatya Çiçeği: Papatya Çiçeğinde de ayçiçeğinde olduğu gibi bir altın oran mevcuttur.
3) İnsan Kafası: Bildiğiniz gibi her insanın kafasında bir ya da birden fazla saçların çıktığı düğüm noktası denilen bir nokta vardır. İşte bu noktadan çıkan saçlar doğrusal yani dik değil, bir spiral, bir eğri yaparak çıkmaktadır. İşte bu spiralin ya da eğrinin tanjantı yani eğrilik açısı bize altın oranı verecektir.
4) İnsan Vücudu: İnsan Vücudunda Altın Oran'ın nerelerde görüldüğüne bakalım:
a) Kollar: İnsan vücudunun bir parçası olan kolları dirsek iki bölüme ayırır.(Büyük(üst) bölüm ve küçük(alt) bölüm olarak). Kolumuzun üst bölümünün alt bölüme oranı altın oranı vereceği gibi, kolumuzun tamamının üst bölüme oranı yine altın oranı verir.
b) Parmaklar: Ellerimizdeki parmaklarla altın oranın ne alakası var diyebilirsiniz. İşte size alaka... Parmaklarınızın üst boğumunun alt boğuma oranı altın oranı vereceği gibi, parmağınızın tamamının üst boğuma oranı yine altın oranı verir.
5) Tavşan: İnsan kafasında olduğu gibi tavşanda da aynı özellik vardır.
6) Mısır Piramitleri: İşte size Altın Oran'ın en eski örneklerinden biri... Şimdi ne alaka Altın Oran ve Milattan Önce yapılan Mısır Piramitleri? Alaka şu; Her bir piramidin tabanının yüksekliğine oranı evet yine altın oranı veriyor.
7) Leonardo da Vinci: Bilindiği gibi Leonardo da Vinci Rönesans devri ünlü ressamlarındandır. Şimdi bu ünlü ressamın çizmiş olduğu tabloları inceleyelim.
a) Mona Lisa: Mona Lisa'nın başının etrafına bir dikdörtgen çizdiğinizde ortaya çıkan dört kenar bir altın dikdörtgendir. Bu dikdörtgeni, göz hizasında çizeceğiniz bir çizgiyle ikiye ayırdığınızda yine bir altın oran elde edersiniz. Resmin boyutları da altın oran oluşturmaktadır.
b) Aziz Jerome: Yine tablonun boyunun enine oranı bize altın oranı verir.
8) Picasso: Picasso da Leonardo da Vinci gibi ünlü bir ressamdır. Ve resimlerinde bu oranı kullanmıştır.
9) Çam Kozalağı: Çam kozalağındaki taneler kozalağın altındaki sabit bir noktadan kozalağın tepesindeki başka bir sabit noktaya doğru spiraller (eğriler) oluşturarak çıkarlar. İşte bu eğrinin eğrilik açısı altın orandır.
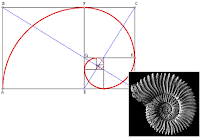
10) Deniz Kabuğu: Denize çoğumuz gitmişizdir. Deniz kabuklarına dikkat edenimiz, belki de koleksiyon yapanımız vardır. İşte deniz kabuğunun yapısı incelendiğinde bir eğrilik tespit edilmiş ve bu eğriliğin tanjantının altın oran olduğu görülmüştür.
11) Tütün Bitkisi: Tütün Bitkisinin yapraklarının dizilişinde bir eğrilik söz konusudur. Bu eğriliğin tanjantı altın orandır.
12) Eğrelti Otu: Tütün Bitkisindeki aynı özellik Eğrelti Otu'nda da vardır.
13) Salyangoz: Salyangozun Kabuğu bir düzleme aktarılırsa, bu düzlem bir dikdörtgen oluşturur. İşte bu dikdörtgenin boyunun enine oranı yine altın oranı verir.
15)Mimar Sinan:Mimar Sinan'ın da bir çok eserinde bu altın oran görülmektedir. Mesela Süleymaniye ve Selimiye Camileri'nin minarelerinde bu oran görülmektedir.
1) Ayçiçeği: Ayçiçeği'nin merkezinden dışarıya doğru sağdan sola ve soldan sağa doğru tane sayılarının birbirine oranı altın oranı verir.
2) Papatya Çiçeği: Papatya Çiçeğinde de ayçiçeğinde olduğu gibi bir altın oran mevcuttur.
3) İnsan Kafası: Bildiğiniz gibi her insanın kafasında bir ya da birden fazla saçların çıktığı düğüm noktası denilen bir nokta vardır. İşte bu noktadan çıkan saçlar doğrusal yani dik değil, bir spiral, bir eğri yaparak çıkmaktadır. İşte bu spiralin ya da eğrinin tanjantı yani eğrilik açısı bize altın oranı verecektir.4) İnsan Vücudu: İnsan Vücudunda Altın Oran'ın nerelerde görüldüğüne bakalım:
a) Kollar: İnsan vücudunun bir parçası olan kolları dirsek iki bölüme ayırır.(Büyük(üst) bölüm ve küçük(alt) bölüm olarak). Kolumuzun üst bölümünün alt bölüme oranı altın oranı vereceği gibi, kolumuzun tamamının üst bölüme oranı yine altın oranı verir.
b) Parmaklar: Ellerimizdeki parmaklarla altın oranın ne alakası var diyebilirsiniz. İşte size alaka... Parmaklarınızın üst boğumunun alt boğuma oranı altın oranı vereceği gibi, parmağınızın tamamının üst boğuma oranı yine altın oranı verir.
5) Tavşan: İnsan kafasında olduğu gibi tavşanda da aynı özellik vardır.
6) Mısır Piramitleri: İşte size Altın Oran'ın en eski örneklerinden biri... Şimdi ne alaka Altın Oran ve Milattan Önce yapılan Mısır Piramitleri? Alaka şu; Her bir piramidin tabanının yüksekliğine oranı evet yine altın oranı veriyor.
7) Leonardo da Vinci: Bilindiği gibi Leonardo da Vinci Rönesans devri ünlü ressamlarındandır. Şimdi bu ünlü ressamın çizmiş olduğu tabloları inceleyelim.
a) Mona Lisa: Mona Lisa'nın başının etrafına bir dikdörtgen çizdiğinizde ortaya çıkan dört kenar bir altın dikdörtgendir. Bu dikdörtgeni, göz hizasında çizeceğiniz bir çizgiyle ikiye ayırdığınızda yine bir altın oran elde edersiniz. Resmin boyutları da altın oran oluşturmaktadır.
b) Aziz Jerome: Yine tablonun boyunun enine oranı bize altın oranı verir.
8) Picasso: Picasso da Leonardo da Vinci gibi ünlü bir ressamdır. Ve resimlerinde bu oranı kullanmıştır.
9) Çam Kozalağı: Çam kozalağındaki taneler kozalağın altındaki sabit bir noktadan kozalağın tepesindeki başka bir sabit noktaya doğru spiraller (eğriler) oluşturarak çıkarlar. İşte bu eğrinin eğrilik açısı altın orandır.
10) Deniz Kabuğu: Denize çoğumuz gitmişizdir. Deniz kabuklarına dikkat edenimiz, belki de koleksiyon yapanımız vardır. İşte deniz kabuğunun yapısı incelendiğinde bir eğrilik tespit edilmiş ve bu eğriliğin tanjantının altın oran olduğu görülmüştür.
11) Tütün Bitkisi: Tütün Bitkisinin yapraklarının dizilişinde bir eğrilik söz konusudur. Bu eğriliğin tanjantı altın orandır.
12) Eğrelti Otu: Tütün Bitkisindeki aynı özellik Eğrelti Otu'nda da vardır.
13) Salyangoz: Salyangozun Kabuğu bir düzleme aktarılırsa, bu düzlem bir dikdörtgen oluşturur. İşte bu dikdörtgenin boyunun enine oranı yine altın oranı verir.
15)Mimar Sinan:Mimar Sinan'ın da bir çok eserinde bu altın oran görülmektedir. Mesela Süleymaniye ve Selimiye Camileri'nin minarelerinde bu oran görülmektedir.